Tuesday, December 15, 2020
Friday, September 25, 2020
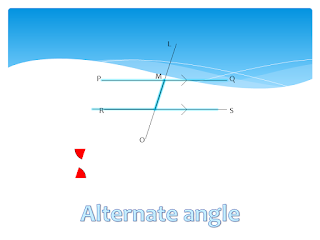
Thursday, September 24, 2020
Friday, September 18, 2020
Friday, September 11, 2020
Tuesday, September 1, 2020
Friday, August 28, 2020
Saturday, August 22, 2020
Monday, August 17, 2020
Monday, July 6, 2020
Thursday, June 25, 2020
Tuesday, June 23, 2020
Monday, June 22, 2020
Saturday, June 20, 2020
Thursday, June 18, 2020
Saturday, May 30, 2020
सरकारी जागिर
यो एउटा निश्चित radius भएको circle हो जुन ५८ वर्षसम्म त्यसको center लाई परिवर्तन गर्न सकिदैन । radius लाई क्षमता अनुसार बढाउन त सकिन्छ तर जति नै बढ्यो उति नै भार थप्छ ।
तर निजी जागिरको centre जता पनि लान सकिन्छ यसकारण जुन क्षेत्र चाहिएको हो सानो radius को circle बनाएर त्यो क्षेत्र आफ्नो बनाउन सक्छौ ।
तर निजी जागिरको centre जता पनि लान सकिन्छ यसकारण जुन क्षेत्र चाहिएको हो सानो radius को circle बनाएर त्यो क्षेत्र आफ्नो बनाउन सक्छौ ।
Saturday, April 4, 2020
Equation of a plane through the intersection of two planes
In
the above figure, thick black and thin
black line represents the 2D form of two planes through which a black dotted
plane passes . and the equation of the thick black line and thin line plane are
a1x+b1y+c1z+d1=0 and a2x+b2y+c2z+d2=0
respectively. Here we have to find the
equation of black dotted plane. Let , OP , PQ and OR are constructed so that
they are normals of black dottted, thin black and thick black plane respectively.
Let the coordinate of O, R, P are (x3,y3,z3),
(x2,y2,z2)
and (x1,y1,z1) repectively. Then since
by definition of plane , the a1, b1 and c1 represents the direction ratio of the normal
of thick black plane. As we assume that OR is also the normal then direction
ratio of OR is
(x3-x2, y3-y2, z3-z2) so OR is also normal so it is parallel to any
normal of that plane so we have following relation
Then we have , x3-x2=ka1,
y3-y2=kb1, z3-z2=kc1
Here PQ is the normal of the thin black
plane which is also parallel to PR so PR is parallel to any normal of that
plane so by similar as above we get
Now the equation of black dotted plane
since it passes through (x3,y3,z3)
We have a(x-x3)+b(y-y3)+c(z-z3)=0 ………..(1)where a, b, c are the direction ratio
of the normal i.e OP of the required plane.
But By figure the direction ratio of OP is (x3-x1,
y3-y1, z3-z1 )
\a= x3-x1=x3-x2+x2-x1=ka1+ma2, similarly b= kb1+mb2 and c= kc1+mc2
Now from (1)
(ka1+ma2 )(x-x3)+
(kb1+mb2 )(y-y3)+ (kc1+mc2
)(z-z3)=0
Or,
(a1+λa2 )(x-x3)+ (b1+λb2
)(y-y3)+ (c1+λc2 )(z-z3)=0 where
Or,
a1x-a1x3+λa2(x-x3)+b1y-b1y3+λb2(y-y3)+c1z-c1z3+λc2(z-z3)=0
Or,
a1x+b1y+c1z+λ(a2x+b2y+c2z)-{(a1x3+b1y3+c1z3)+λ(a2x3+b2y3+c2z3)}=0……..(2)
Now
since (x3,y3,z3) also passes through two
planes a1x+b1y+c1z+d1=0 and a2x+b2y+c2z+d2=0
so
a1x3+b1y3+c1z3+d1=0 ………..´1
add above we get(a1x3+b1y3+c1z3)+λ(a2x3+b2y3+c2z3)=-(d1+λd2)……..(3)
now from (2) and (3) we get
a1x+b1y+c1z+λ(a2x+b2y+c2z)+
(d1+λd2)=0
\ a1x+b1y+c1z+d1+λ(a2x+b2y+c2z+d2)=0 is the required plane .
Subscribe to:
Comments (Atom)
-
Consider the motion of a small rectangular parallelepiped in viscous fluid with centre at P(x,y,z) and it’s edges of length d x, d y, ...
-
Solution: In this figure 1 , a uniform solid cylinder is placed horizontally on the plane BOCD Which makes an angle α with the hor...
-
Exercise . 1. a) If profit is P% and cost price is C.P. What will be the selling price ? b) If loss is L% and cost price is C.P. What...